这本书是什么?
这本书是一本科普著作,从最抽象的数开始讲起,接下来开始空间和时间,随后以微观世界和宏观世界结束了这本书的内容。正如《资本论》一样,从商品交换开始,推导出一系列的世界现象。这正是我们所追求的目标之一。
这本书的作者呢?
| 时间 | 事件 |
|---|---|
| 1904 | 出生于俄国敖德萨市 |
| 1914-1920 | 敖德萨师范学校 |
| 1926 | 毕业于列宁格勒大学 |
| 1928 | 获得苏联列宁格勒大学哲学博士学位 |
| 1928-1932 | 在哥本哈根大学和剑桥大学师兄波尔和卢瑟福,进行研究工作 |
| 1931 | 回答列宁格勒大学任教授 |
| 1933 | 在巴黎居里研究所 |
| 1934 | 移居美国,密执安大学讲师 |
| 1954 | 任加利福尼亚大学伯克利分校教授 |
| 1956 | 任科罗多大学教授 |
可以说,这个人的一生大部分时间都是在进行科研的道路上进行工作,是一位真正的科研工作人员
本书第一部分的内容
关于这本书呢,有非常多的内容,如果想要将其整合起来呢,暂时有点困难。特别是关于微观世界和宏观世界的内容,有不少自己都不够了解,仅仅是囫囵吞枣版的看完了。所以本次分享将会专注于前面两章
大数
问题1,什么是大数?
第一类,有限的,但是超出我们认知范围之外的数
第二类,无限的,无穷大的数
第一类大数虽然有限,但是也会超出我们一般人的想象。比如说一车沙子里面有多少粒沙子?天上有多少星星?海里有少水分子?$$1+2^1+2^2+2^3+···+2^{63}$$粒麦子
这里就有一个我们都听过的一个故事:
根据古老的传说,舍罕王打算重赏象棋*的发明人和进贡者,宰相西萨·班·达依尔(Sissa Ben Dahir)。这位聪明大臣的胃口看来并不大,他跪在国王面前说:“陛下,请您在这张棋盘的第一个小格内,赏给我一粒麦子;在第二个小格内给两粒,第三格内给四粒,照这样下去,每一小格内都比前一小格加一倍。陛下啊,把这样摆满棋盘上所有 64 格的麦粒,都赏给您的仆人罢!”
“爱卿。你所求的并不多啊。”国王说道,心里为自己对这样一件奇妙的发明所许下的慷慨赏诺不致破费太多而暗喜。“你当然会如愿以偿的。”说着,他令人把一袋麦子拿到宝座前。
计数麦粒的工作开始了。第一格内放一粒,第二格内放两粒,第三格内放四粒,……还没到第二十格,袋子已经空了。一袋又一袋的麦子被扛到国王面前来。但是,麦粒数一格接一格地增长得那样迅速,很快就可以看出,即便拿来全印度的粮食,国王也兑现不了他对西萨·班·达依尔许下的诺言了,因为这需要有$$1+2^1+2^2+2^3+···+2^{63}$$18,446,744,073,709,551,615 颗麦粒呀!
这类数字超出了我们的认知,完全想象不出来,所以被称作大数
第一类大数虽然大,但是仍然是可以计量的,只是我们缺乏了想象。但是第二类大数我们却没有办法计量了都。
比如说,偶数、奇数的个数;一条线上所有几何点的个数;一个几何面上的结合点数目……
问题2,第二类大数都是无穷,如何比较?
我们可以给两组无穷大数列中的各个数一一配对。如果最后这两组都一个不剩,这两组无穷大就是相等的;如果有一组还有些数没有配出去,这一组就比另一组大些,或者说强些。
比如,奇数和偶数哪个多呢?
| 奇数 | 1 | 3 | 5 | …… |
|---|---|---|---|---|
| 偶数 | 2 | 4 | 6 | …… |
所以奇数和偶数一样多
那么,整数=奇数+偶数;那么偶数和整数谁多呢?
| 整数 | 1 | 2 | 3 | …… |
|---|---|---|---|---|
| 偶数 | 2 | 4 | 6 | …… |
结果发现,偶数和整数一样。怎么解释呢?无穷大的世界和普通世界不一样,在无穷大的世界当中,无穷的一部分还是无穷。在无穷大的世界当中,部分可能等于整体。
问题3,第二类数都是无穷,似乎都是相等的,有什么意义呢?
第二类大数的确是又穷的,但是两者之间却存在大小。
比如说,比如说有理数的数量就比整数多。因为其中存在无理数,无限不循环小数等等。
在本书中,作者讲无穷数列进行了分类,举出了三种无穷大的数
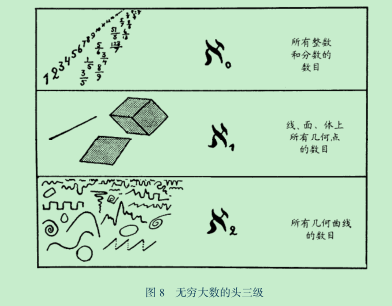
虚数
在这里需要思考一下我们上学过程中学到的数学,数按照大小进行排序
自然数,整数,有理数,实数,复数
前面三个都好理解,前面四个都好理解,但是第五个复数当中却包含实数和虚数。
问题1,虚数是啥?
对负数进行开方运算,便是虚数。这个东西有啥用嗯?
有下面一题:
是否有可能将 10 分成两部分,使两者的乘积等于 40
这个问题呀,在有理数的范围内没有办法进行解答。但是16 世纪的意大利数学家卡尔丹却把这个东西给解答了出来。
$$
(5+sqrt{-15})+(5-sqrt{-15})=10
$$
$$
(5+sqrt{-15}) times (5- sqrt{-15})=40
$$
但是虚数还是很神秘,留待后人思考。
问题2 虚数的几何解释?
在直角坐标当中,实数是横坐标,虚数是纵坐标
- 所有的实数(正数和负数)都对应于横轴上的点;
- 而纯虚数则对应于纵轴上的点。
- 一个数乘以 i,在几何上相当于逆时针旋转 90°。
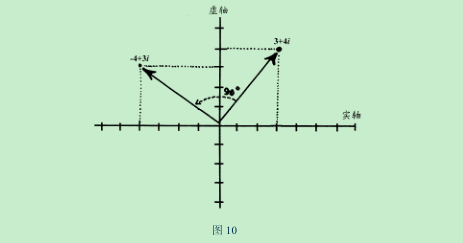
所以,这里就能够解释一下上面那道题目了

这就是上面那道题的物理图像
问题3,虚数的使用方向?
在四维空间中,表示时间的部分。
读书感受
不要觉得某些事情是确定的,反向思考,总会有突破
比如说,当正数在的时候,有人提出,有没有负数?没有吧,这玩意没啥用?有用,可以用来计量缺失的量,比如说你欠别人的钱。
有理数存在的时候,有人提问,有没有无理数?没有办法,怎么可能?结果发现了$$sqrt{2}$$
实数在的时候,有人提出,有没有虚数?负数开根号有没有意义?没有,但是发现了负数开根号出现的虚数能够用来解决四维时空当中的内容。
看书最重要的是要看科学发展当中的突破点,并且以此来指导接下来的思考
要看名人是如何提出和解决问题的。
- 比如说,提出大数有没有办法比较的康托尔
- 提出无理数的希伯索斯
- 把虚数用来解题的卡尔丹
- ……
这些人的思考,是我们未来解决问题的思维源泉。
